9.3 相关性

解决上一节协方差遇到的问题的方法是用标准分数来代替原始的值，计算两个标准分数的乘积： $p_i = \frac{x_i-\mu_X}{\sigma_X}\frac{y_i-\mu_Y}{\sigma_Y}$ 这些乘积的均值为： $\rho = \frac{1}{N}\sum p_i$ 这个值称为皮尔逊相关系数（Pearson's correlation），用以纪念现代统计学创立者卡尔·皮尔逊。相比于协方差，相关系数很容易计算，更重要的是，它的结果更容易解释。相关系数的单位为1。

相关系数ρ的取值为-1到1之间。我们改写一下ρ的表达形式就可以很容易得到这个结果： $\rho = \frac{\mathcal{Cov}(X,Y)}{\rho_X\rho_Y}$ 将离差项代入公式，可得 $\rho = \frac{\sum dx_idy_x}{\sum dx_i \sum dy_i}$ 利用著名的柯西—施瓦兹不等式〔1〕（Cauchy-Schwarz inequality）即可证明ρ2≤1，故而有-1≤ρ≤1。

〔1〕参见http://wikipedia.org/wiki/Cauchy-Schwarz_inequality。

ρ的绝对值的大小代表两个变量相关的程度。当ρ=1时，两个变量完全相关，即如果我们知道了其中一个变量的值，就可以精确预测另一个变量的值。ρ=-1时也是同样的情况，只是两个变量是完全负相关而已。

现实中大部分的相关都没有这么完全，但是相关系数仍然提供了一些有用的信息。例如，在知道了一个人的身高后，我们猜测这个人的体重，虽然我们不大可能猜对，但是相比于不知道身高的情况下，我们依然可以猜测得更准确。皮尔逊相关系数衡量了我们能够多准确地猜测结果。

如果ρ=0，这是不是意味着两个变量之间毫无关系呢？不幸的是我们不能得出这个结论。皮尔逊相关系数只是衡量两个变量之间的线性关系。如果两个变量之间的关系不是线性的，那么ρ可能低估两个变量之间的相关性。

图9-1来源于http://wikipedia.org/wiki/Correlation_and_dependence。图中展示了一些精心构造的数据的散点图及对应的相关系数。

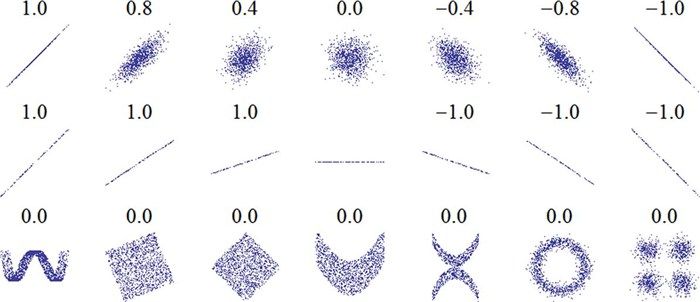
图9-1 具有一定相关性的示例数据集

图中第一行展示了几组有线性相关性的数据的相关系数，我们可以直观地了解这些相关系数大约会对应到什么水平的关系。第二行展示了完全相关的数据的相关系数，这里我们发现相关系数跟斜率是无关的（稍后就会讲到估计斜率）。第三行展示了一些有明显相关性的数据，但由于这些关系不是线性的，这里的皮尔逊相关系数等于0。

这提醒我们别盲目地相信这个系数，在计算相关系数之前，一定要画个散点图观察一下数据。

习题9-2

请编写一个计算相关系数的函数Corr，该函数可接受两组数据。提示：这里可以用到之前的函数thinkstats.Var和Cov。

可以通过计算Corr(X, X)是否等于1来测试函数是否正确。http://thinkstats.com/correlation.py提供了一个答案。