4.1 指数分布

我首先介绍最简单的指数分布（exponential distribution）。举个例子，观察一系列事件之间的间隔时间（interarrival time）。若事件在每个时间点发生的概率相同，那么间隔时间的分布就近似于指数分布。

指数分布的CDF是：

CDF(x)=1−e−λxCDF(x)=1-e^{-\lambda x}

参数λ决定了分布的形状。图4-1中是λ=2时的CDF。

通常，指数分布的均值是1/λ，所以这个分布的均值是0.5。分布的中位数是log(2)/λ，大概等于0.35。

来看一个近似指数分布的例子，我们看看宝宝出生时间的间隔。1997年12月18日，澳大利亚布里斯班的医院总共出生了44个宝宝〔1〕。这44个宝宝的出生时间数据在当地的历史文件中有记录，可以从http://thinkstats.com/babyboom.dat下载到这个数据。

〔1〕这个例子的信息和数据来自Dunn, “A Simple Dataset for Demonstrating Common Distributions,” Journal of Statistics Education v.7, n.3 (1999)。

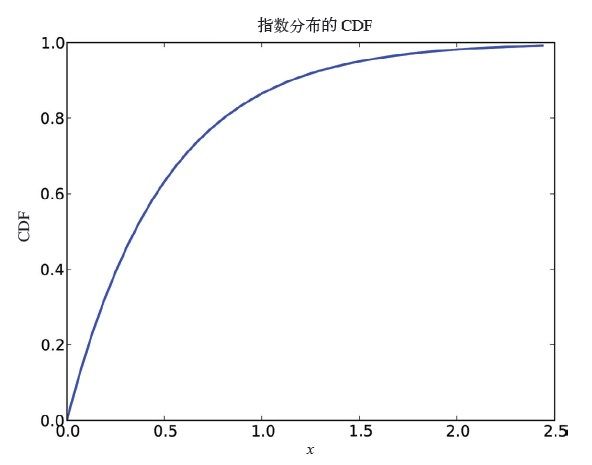
图4-1 指数分布的CDF

图4-2中是间隔时间的CDF，单位是分钟。这看上去跟指数分布的形状很像，但我们如何才能确定这就是一个指数分布？

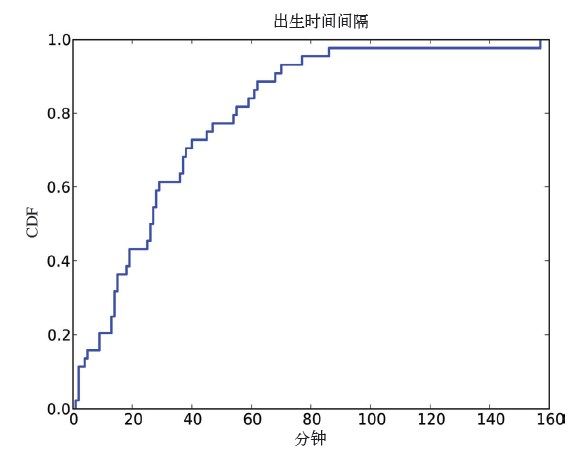
图4-2 间隔时间的CDF

一种办法是画出取对数后的互补累积分布函数（Complementary CDF，CCDF）：1 - CDF(x)。如果数据服从指数分布，这应该是一条直线。让我们看看为什么会这样。

指数分布的数据集的CCDF如下：

y≈e−λxy \approx e-\lambda x

两边取对数得到：

logy≈−λxlog_y \approx -\lambda x

所以，在对y轴上的值取对数后，CCDF是一条斜率为−λ的直线。

图4-3是y轴取对数后的间隔时间的CCDF。图中并不是一条严格意义上的直线，说明指数分布还只是一个近似。也就是说，以下假设并不完全正确：宝宝在一天中各个时间出生的概率一样。

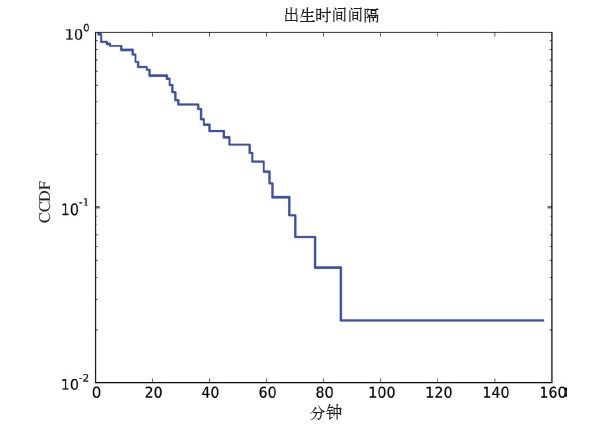
图4-3 间隔时间CCDF

习题4-1

在n较小时，经验分布不会很好地符合连续分布。评价两者间相似性的一个方法是从连续分布中生成样本，看看生成的样本跟数据的匹配情况。

random模块中的expovariate函数可以为给定λ生成服从指数分布的随机数。用这个函数生成44个服从随机分布且均值为32.6的数。画出其y取对数后的CCDF图，将其与图4-3做比较。

提示：可以用pyplot.yscale画出取对数后的y轴。

也可以用myplot中的Cdf函数绘制y取对数后的CCDF，Cdf函数有一个选项complement，用于判断是绘制CDF还是CCDF，还有两个用于数轴转换的字符串选项xscale和yscale：

myplot.Cdf(cdf, complement=True, xscale='linear', yscale='log')

习题4-2

收集你班上同学的生日，先排序，然后以天为单位计算同学生日的时间间隔。画出间隔时间的CDF和y轴取对数后的CCDF，它们看上去像是指数分布吗？