2.2 方差
既然一个值无法概括南瓜的重量,那两个值应该会好一些:均值和方差。
均值是为了描述集中趋势,而方差则是描述分散情况。一组值的方差等于:
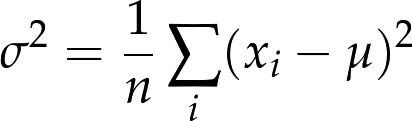
其中叫做离均差(deviation from the mean),因此方差为该偏差的方均值,这也是用表示的原因。方差的平方根叫做标准差。
方差本身不太好解释,其中一个问题就是它的单位很奇怪。在南瓜重量的例子中,度量单位是磅,所以方差的单位就是磅的平方。标准差的含义就明确多了,在上例中单位为磅。
习题2-1
先从http://thinkstats.com/thinkstats.py下载脚本文件,其中的函数在整本书中都会有用。这些函数的文档可以参考这里http://thinkstats.com/thinkstats.html。
编写一个Pumpkin函数,并调用thinkstats.py中的函数计算上一节中南瓜重量的均值、方差和标准差。
习题2-2
重用survey.py和first.py中的代码计算第一胎宝宝的怀孕周期和其他宝宝的怀孕周期的标准差。这两组数据的分散情况一样吗?
跟标准差的差异相比,均值的差异有多大?对于该差异的统计显著性,这个比较说明了什么?
如果以前接触过方差,你会发现通常我们在依据样本估计方差时,计算公式中使用的除数是n-1,而不是n,这个统计量叫做“样本方差”。第8章我们会再次介绍这个概念。