4.3 正态分布

正态分布也称为高斯分布，因其可以近似描述很多现象而成为最常用的分布。它的“普适性”是有原因的，我们会在6.6节做介绍。

正态分布有很多使其适用于各种分析的特性，但CDF并不是其中之一。跟之前看到的分布不一样，我们对于正态分布的CDF还没有一种准确的表达。最常用的一种形式是以误差函数（error function）表示的，误差函数是一种特殊函数，表示为erf(x)：

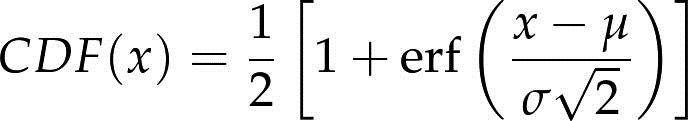
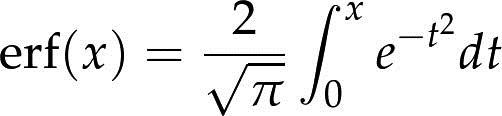
参数μ和σ决定了分布的均值和标准差。

如果这些公式看起来眼花也别担心，在Python中很容易实现这些公式〔1〕。有很多高效准确的方法来近似erf(x)。我实现了一种，可从http://thinkstats.com/erf.py下载，其中提供了erf和NormalCdf两个函数。

〔1〕在Python 3.2中更容易，math模块中就有erf函数。

图4-5是参数μ=2.0，σ=0.5的正态分布的CDF。这种S型曲线就是正态分布的标志。

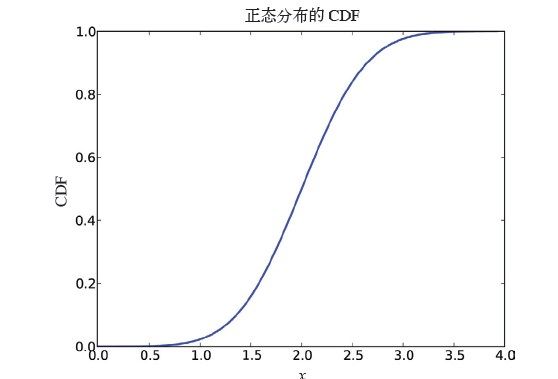
图4-5 正态分布的CDF

在前一章中，我们看过NSFG数据中新生儿体重的分布。图4-6中是所有新生儿体重的经验CDF，以及有着相同均值和方差的正态分布的CDF。

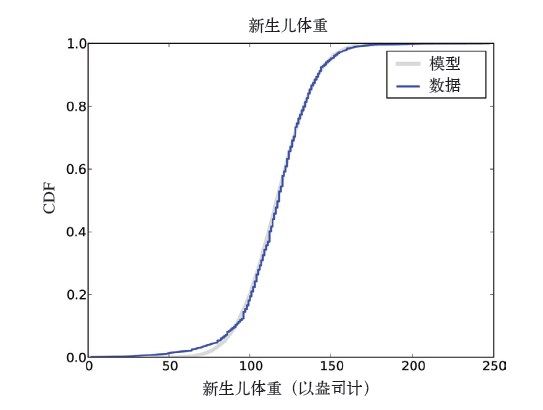
图4-6 服从正态模型的新生儿体重的CDF

对于这个数据集，正态分布是一个不错的模型。模型就是一种有效的简化。此处说它简单实用是因为我们可以用两个参数（μ=116.5和σ=19.9）来总结整个分布，并且所得到的误差（模型和数据之间的区别）很小。

在10百分位以下的部分，数据和模型之间出现了差异，体重较轻的新生儿数量比我们根据正态分布得到的预期值要高一些。如果研究的是早产儿，那么这部分分布的正确性就非常重要，使用正态分布就不合适了。

The Wechsler Adult Intelligence Scale是一个智商测试〔2〕。我们对结果作变换，这样分数在一般人群中的分布就是正态的，参数为μ=100和σ=15。

〔2〕可以在闲暇时间了解一下，看看该智商测试是否吸引你，你觉得测试结果可靠吗？

用erf.NormalCdf函数查看正态分布中罕见事件的频率。人群中有多大比例的人智商高于均值？高于115、130、145的分别是多少？

“六西格玛”事件就是超出均值6个标准差的值，所以六西格玛智商是190。在全世界60亿人中，智商超过190的人有多少〔3〕？

〔3〕这方面的详细信息请阅读http://wikipedia.org/wiki/Christopher_Langan。

画出所有新生儿怀孕周期的CDF。看上去像正态分布吗？

计算样本的均值和方差，根据这两个参数画出正态分布。使用该正态分布对数据建模合适吗？如果用两个统计量来总结这个分布，应该选哪两个统计量？