5.7 贝叶斯定理
贝叶斯定理(Bayes's theorem)描述的是两个事件的条件概率之间的关系。条件概率通常写成P(A|B),表示的是在事件B已发生的情况下事件A发生的概率。贝叶斯定理用公式表达如下:
为了说明这个公式的正确性,不妨把事件A和事件B同时发生的概率写作P(AB):
同样,
也是成立的,因此:
两边都除以P(B)就得到了贝叶斯定理〔1〕。
贝叶斯定理通常用于解释某一特定现象的证据E如何影响假设H的概率:
这个等式的意思是:在看到E之后H的概率P(H|E),等于看到该证据前H的概率P(H),乘以假设H为真的情况下看到该证据的概率P(E|H)与在任何情况下看到该证据的概率P(E)的比值P(E|H)/P(E)。
这种解读贝叶斯定理的方法叫做“历时性”(diachronic)解读,因为这描述了假设成立的概率随时间发生的变化,这种变化通常都是因为出现了新证据。在这种情况下,P(H)称为先验概率(prior probability),而P(H|E)称为后验概率(posterior probability)。P(E|H)是证据的似然值(likelihood of evidence),P(E)是归一化常量(normalization constant)。
贝叶斯定理的一个经典应用就是解读临床检测。例如,学校和工作单位违禁药物检查正变得越来越普遍(详见http://aclu.org/drugpolicy/testing)。采用这些检查的用人单位希望这些检查是敏感的,即当样品中有药物(或相关代谢物)时要得到一个阳性结果,而且要是特异的,即当样品中没有药物时得到阴性结果。
根据美国医学协会杂志(Journal of the American Medical Association)的估计〔2〕,常规药检的灵敏度大约是60%,特异性大概是99%。
〔2〕我是从Gleason和Barnum的“Predictive Probabilities In Employee Drug-Testing”一文中看到这些数据的,网址是http://piercelaw.edu/risk/vol2/winter/gleason.htm。
现在假设这种常规检查适用于实际使用违禁药物比例为5%的职工人群,那么检查结果为阳性的雇员中有多少真正使用了违禁药物?
在贝叶斯理论中,我们要计算的就是当检查结果为阳性时,用药的概率P(D|E)。根据贝叶斯定理:
先验概率P(D)就是我们看到检查结果之前用药的概率(即5%),似然值P(E|D)就是使用了违禁药的情况下检查结果为阳性的概率(即灵敏度)。
计算归一化常量P(E)会稍微困难点。要考虑两个概率,P(E|D)和P(E|N),其中N代表受试者没有用药的假设:
假阳性的概率P(E|N)跟特异性是互补的,即1%。把这些放在一起,我们得到:
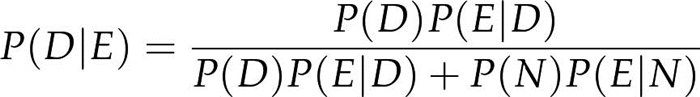
代入相应的值,我们得到P(D|E) = 0.76,这意味着每四个检查结果为阳性的人中大概有一个是被冤枉的。
习题5-14
写个程序,输入参数是用药的实际比例、监测的灵敏度和特异性,然后根据贝叶斯定理计算P(D|E)。
假设将同样的检测用到用药比例为1%的人群,检查结果为阳性的人真正用药的概率是多少?
习题5-15
这个练习来自http://wikipedia.org/wiki/Bayesian_inference。
假设有两碗饼干。一个碗中有10片巧克力饼干和30片普通饼干,而另一个碗中巧克力饼干和普通饼干各有20片。我们的朋友Fred随机选了一个碗,然后随机地从中取出一片饼干。那么Fred从第一个碗中取出普通饼干的概率是多少?
习题5-16
蓝色的M&M巧克力豆是1995年上市的。在那之前,一袋混合M&M巧克力豆的组成是30%棕色、20%黄色、20%红色、10%绿色、10%橙色和10%褐色;1995年之后,其组成是24%蓝色、20%绿色、16%橙色、14%黄色、13%红色和13%棕色。
我的一个朋友有两袋M&M,其中一袋是1994年产的,另一袋是1996年产的。但他没有告诉我到底哪一袋是1994年的,哪一袋是1996年的。现在朋友从两袋中各取出一粒巧克力豆,一粒是黄色,一粒是绿色。黄色巧克力豆来自1994年那袋的概率是多少?
习题5-17
这个练习改编自MacKay的Information Theory, Inference, and Learning Algorithms一书。
猫王Elvis Presley有一个双胞胎兄弟,但不幸在出生时就夭折了。根据维基百科上对双胞胎的介绍:
双胞胎占全世界人口的比例大概是1.9%,同卵双胞胎的比例大概是0.2%,占所有双胞胎的8%。
那么,Elvis与夭折的兄弟为同卵双胞胎的概率是多少?